Orbits and Inverse Squares

One of the milestones on the journey from superstition to science was Johannes Kepler's realization, in 1609, that planetary orbits are shaped like ellipses with the sun at one focus. Kepler based his theory on recent observations by Tycho Brahe; up until then, everybody thought planetary orbits were circles.

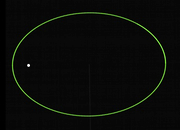elliptical orbit Here's a diagram of an ellipse with one focus marked. (The ellipse in the diagram is exagerrated for clarity; most planetary orbits are nearly circular.)

Seventy-five years later, in 1684, Isaac Newton published the first proof that the elliptical orbit of a planet is the result of a central force proportional to the inverse square of the planet's distance from the sun. That proof, which was so difficult that even Richard Feynman couldn't make it easy to understand, was purely geometrical. More recent proofs use calculus, which makes them simpler, but still not so easy to visualize. You can find many expositions of these proofs on the World Wide Web.

Instead of yet another proof, I've made a step-wise computer simulation that uses inverse-square attraction to generate an elliptical orbit. The simulation is no substitute for a mathematical proof, but does make it easier to see what's happening.

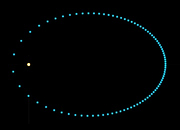orbit using inverse squares Here's the simulated orbit of an imaginary planet moving under an inverse-square attraction to its sun. The simulation not only generates an elliptical orbit, but, because the time from each step to the next is the same, it also shows how the planet speeds up and slows down as it draws nearer to and farther from the sun. This link shows an animation of the simulation.

How it works

The simulation starts with a specified location and velocity of the planet with respect to the sun at the origin. The simulation then executes a repeated sequence of steps for successive equal time intervals. At each step it calculates the distance of the planet from the sun, the acceleration based on the inverse square of that distance, a new velocity incorporating that acceleration, and a new position based on that velocity.

Full disclosure: Because the simulation uses finite steps, it generates only an approximation of 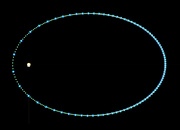orbit using inverse squares the actual ellipse. More and smaller steps give a closer approximation, so I actually ran the simulation with six times as many points as shown here, then used every sixth point for the animation.

[X] Close.